Introduction
I recently discovered that the concepts of precision, recall, sensitivity and specificity are very much important to what I am currently working on. Those are equally important but not for a single domain. Instead we have different indicators for different domains. For example, in information retrieval, precision and recall are two important measures that need to be taken into account when evaluate a search system. In pattern recognition and machine learning, precision and recall are important as well but there is a slight difference when interpret them. On the other hand, sensitivity and specificity are alternations to precision and recall when it comes to medical application. In this writing, we aim to explain why there exist those differences in the first place.
In order to begin, first we look at the confusion matrix to understand where terms TP, FP, TN, and FN come from, and second, look at the Venn digram that perfectly portraits the territories of TP, FP, TN, and FN within the search space.
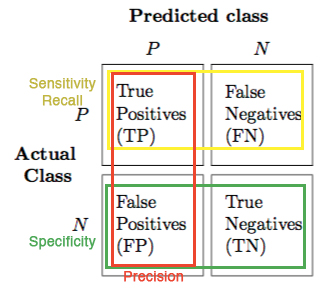
The confusion matrix of the search space
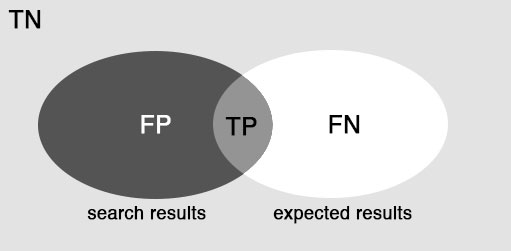
The Venn diagram of the confusion matrix (I guess it better applies to information retrieval)
And mathematically, precision, recall, sensitivity and specificity are denoted as below.
\[Precision = \frac{TP}{TP + FP} \\ \\ Recall = Sensitivity = \frac{TP}{TP + FN} \\ \\ Specificity = \frac{TN}{TN + FP}\]Precision
I found that we can easily understand the intuitive concept of precision by simply looking at the Venn diagram. Simply speaking, precision is the ratio between the documents that match the user expectation and the total number of documents returned by the system. One cay say that the higher the precision, the better. But it is always true because a system can cheat the precision score up to 100% by only returning documents about which it is extremely confident. By doing this, the amount of returned documents is severely reduced, making it so resistant to FP.Look at the figure below, because the space of returned documents is so small, it can fall within the space of the expected documents easily. What is the problem with that? Because the amount of search result is extremely small, the information is likely inadequate to support the user tasks. Mathematically, we have \(TP \rightarrow 1\), \(FP \rightarrow 0\), thus \(\frac{TP}{TP + FP} \rightarrow 1\).

We can cheat the precision result
Recall and Sensitivity
We can also grasp the concept of recall and sensitivity smoothly through the Venn diagram observation. Both recall and sensitivity can be understand as the ratio between the documents that match the user expectation and the total number of expected documents from the user. Intuitively speaking, recall and sensitivity are big indicators for how much good information that a system really misses, whereas precision is an indicator for how much good information in the search result the user can use. We can also cheat the recall/sensitivity score by getting the system to add up the number of returned documents, making the search result overwhelmingly abundant. Then guess who is going have a hard time to filtrate such load of information. Look at the figure below, we can see that by returning an overwhelming amount of information, the system can ensure that its recall/sensitivity is maximized. Mathematically, by doing this we have \(TP \rightarrow 1\), \(FN \rightarrow 0\), therefore \(\frac{TP}{TP + FN} \rightarrow 1\).

We can cheat the precision result
Specificity
To understand the concept of specificity, as oppose to observing the Venn diagram, I found it much more easier to understand by checking the confusion matrix. First of all, one has to understand that by using specificity, he wants to steer the focus of his evaluation towards how good the system can predict negative outcomes( or how good the system can avoid returning irrelevant documents,. That’s the reason why TN is the numerator of the equation in the first place. One can also maximize the specificity score of the system by getting the system return no information at all (or predict all observations are negative). Mathematically, when return no information or predict all are negative, \(FP \rightarrow 0\) and \(TN \rightarrow 1\), then \(\frac{FP}{TN + FP} \rightarrow 1\).
Which one I should use?
We have four metrics to choose, so the question is which one I should. Well I can say that it depends on the problem domain. For example, if we have built a search system, in order to evaluate it, firstly we have to answer some questions: Which criteria we care about most? Do we care about the vast amount of information we ignore (which is TN)? Or do we care about the information we can return (FP + TP + FN)? My answer is I care about the relevant of information my system gives the user rather than the information I can’t return (there is countless amount of information, who cares in the first place). Thus, to evaluate the search system, I would use precision, recall and ignore specificity.
In contrast, suppose we have a diabetes predictive model to evaluate, which metrics should we care about? Do we care if a patient doesn’t have diabetes, but the system predicts positive (TN + FP)? Do we care about if a patient has diabetes, but the system predicts negative (TP + FP)? and so on. My answer is I would use all of three indicators (e.g., precision, recall, specificity) because I guess we have to take into account all of indicators TP, FP, TN and FN. Everything is crucial in this case.
Lastly and interestingly, imagine if we had a system that can exploit all evidences and judge if a suspect guilty. In this case, what we care about most? Do we care if the suspect doesn’t commit the crime but the system judges him guilty (FP)? Or do we care if the suspect does commit the crime but the system judges him not guilty (FN)? Yeah, I guess in this case, we should put more emphasis on FP rather than FN, because putting an innocent person to the jail is also a crime, and letting a guilty suspect go is not as dire as putting innocent person to jail.
** In statistic and relevant fields, usually we put more emphasis on Type I error (e.g., reject \(H_0\) incorrectly (FP)), rather than Type 2 error (e.g., retain a false \(H_0\) (FN)).
The end.